精准教学
以测辅学:智慧教育境域中精准教学的核心机制
以测辅学:智慧教育境域中精准教学的核心机制
彭红超 1, 祝智庭 2
(1.华东师范大学 教育学部 教育信息技术学系, 上海 200062; 2.华东师范大学 开放教育学院, 上海 200062)
[摘 要] 早期精准教学的“以测辅学”机制只注重行为本身,而智慧教育对教与学测评具有新诉求:明白所测构念 的实质意义。对此,本研究从“测量”、“记录”和“决策”等三个要素切入,并以智慧教育上述诉求为导向,结合心理与教 育测量学中的构念理论,深入、全面地透析智慧教育境域中精准教学“以测辅学”的机制与原理 :测量时“以测识学”的原理(所测构念的实质 、流畅度作为计量指标的机理),记录时“以绘视学”的 原 理 ( 频率作为记录指标 、 变 速 图 作 为 记 录图表的机理)和决策时“以评辅学”的原理(变速线作为决策依据的机理 、决策模型及辅助机理 )。 最后,以此为基础 总结了以测辅学机制的具体操作步骤,以期能为精准教学的具体实施提供指导和参考 。
[关键词] 智慧教育; 精准教学; 构念理论; 流畅度; 标准变速图表
[中图分类号] G434 [文献标志码] A
[作者简介] 彭红超 (1987—), 男, 山东临沂人。 博士研究生, 主要从事智慧学习生态、 精准教学研究。 E-mail: hongchao5d@qq.com。 祝智庭为通讯作者,E-mail:ztzhu@dec.ecnu.edu.cn。
智 慧 教 育 (Smarter Education,SerE) 境 域 中 的 精 准教学(Precision Instruction,PI)是从技术赋能层面给 养智慧学习生态的核心机制。 它旨在从教学准确度方 面实现百分百教学,避免由于累积效应导致准确度的 衰减,从而致使智慧学习(Smart Learning,SL)的失败。 信息技术支持的精准教学模式[1]将精准教学表征为包 含“精准确定目标”、“开发材料与设计活动”、“测量与 记录表现”和“数据决策”等四个阶段的循环。 前期,笔 者及所在的团队已对前两个阶段作了翔实的钻研[1-2],本研究作为后续研究,将承接先前成果,开展“测量与记录表现”和“数据决策”阶段的探讨。 “测量与记录 表 现”与“数据决策”的核心理念为“以测辅学”,这也是 智慧教育境域中精准教学的核心机制。 以测辅学包含三个要素:测量、记录与决策。 因此,本研究主要从这 三个要素切入,以智慧教育新诉求为导向,结合心理 与教育测量学中的构念理论,较为深入、全面地透析 精准教学。
一、智慧教育境域中的精准教学机制
早期的精准教学仅仅作为评估任意给定的教学 方法有效性的框架[3]。 随着教育变革的推进,为满足教 师们“更希望有现成的精准教学模式”[4]的诉求,精准 教学已有了相应的发展变化。尽管如此,“以测辅学” 一直是精准教学的核心机制。在数据被日益重视的数 字化时代,以测辅学的核心地位将得到进一步加强和 巩固。与此同时,智慧教育也对精准教学的这一核心机制提出了新的要求。
(一)精准教学以测辅学的核心机制
早期的精准教学作为评估教学方法的框架,旨在通过设计测量过程来追踪学生的学习表现并支持数 据决策[5]。 信息技术支持的精准教学通过采用适当的 技术,生成个性化的精准教学目标,开发适切的教学 材料、设计适宜的教学活动进行教学,并且频繁地测 量与记录学习者的学习表现,以精确判定学习者存在的当前问题及潜在问题,针对判定的问题,采用适当 的数据决策技术以对教学策略进行精准的优化和干 预[1]。 可以看出,信息技术支持的精准教学虽然演变成 为一种个性化教学方法,然而以测辅学仍是它的核心 机制。
以测辅学包含测量、记录和决策等三大要素(如 图 1 所示)。 其中,测量旨在使用测量工具及时甚至实 时地测量学生的学习表现;记录旨在将学生的学习表 现及时甚至实时 地记录在标准变速图表 (Standard Celeration Chart,SCC) 上 ; 决策旨在通过观测标准变 速图表上学生的学习表现蓝图及时甚至实时决策,若 学生存在问题及潜在问题则及时辅助。 测量、记录和 决策自然过渡且循环发生。 对于每次的辅助,均需要 进入新一轮循环以测查辅助效果。 如果辅助成功,则 进入下一目标的学习;如果辅助失败,则进行更专业、 更高级的辅助。 以测辅学摒弃了传统教学中教师凭主 观经验调整教学的方式,转而强调以学生实时表现数 据 为依据辅助教学,这使得教学更加有理、有据。 另 外,以测辅学以学生个体为测量对象。 因此,精准教学 为解决“一人生病,全班吃药”的弊病提供了“对症开 药”的有效方法,以测辅学也诠释了“精准”的内涵。
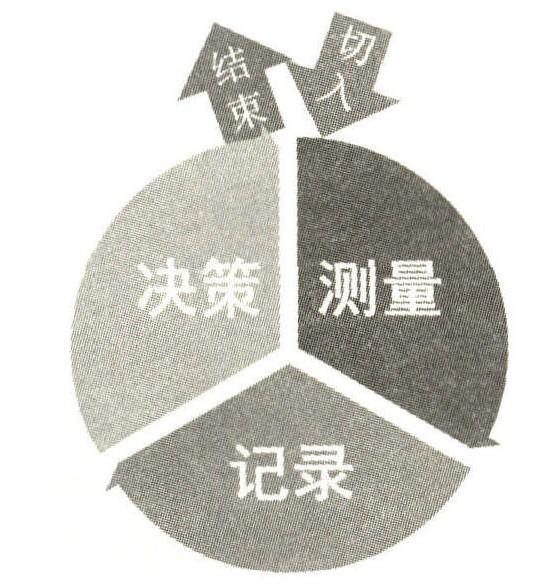
图 1 以测辅学三要素
(二)智慧教育与精准教学核心机制的吻合
智慧教育旨在培养具有良好的价值取向、较强的 行动能力、较好的思维品质、较深的创造潜能的智慧 型人才[6]。 为了实现这一愿景,智慧教育从技术与理念 两个角度对教育教学提出了新要求。 从技术角度讲, 智慧教育需要基于学生的表现数据进行精准决策,诊 断学生学习过程中遇到的问题与难点。 以此为基础, 便可开展有针对性的精准帮学,开展更为灵活的教学 活动,甚至实现教师的精细化分工。 从理念角度讲,智 慧教育不仅注重知识技能的传授,而且更加注重能力 品质的培育。 而知识技能特别是能力品质的培育要依赖于技术的支撑。 因此,智慧教育实现培育智慧型人才的愿景是以学生的表现数据的测评为根基。 这与精 准教学的以测辅学核心机制不谋而合。
精准教学以学习表现的流畅度(Fluency)为学生 学习发展的主要指标[7]。 流畅度具有五大特征[6]:持久 性 (Maintenance)、 耐 久 性 ( Endurance)、 稳 定 性
(Stability)、 应 用 性 (Application)和 生 成 性(Generativity)[8]。 这五大特征分别指示“未来熟练执 行的能力”、“执行必要长时间的能力”、“执行时抗干 扰能力”、“易于用于新情境的能力 ” 以及“ 出现新表 现以解决新问题的能力”。 因此,精准教学的流畅度 指标符合智慧教育对知识技能以及能力品质的标定 需求。
上述两种吻合的情况也是精准教学能够成为从 技术赋能层面给养智慧学习生态的核心机制的主要 原因。
(三)智慧教育对精准教学核心机制的新诉求
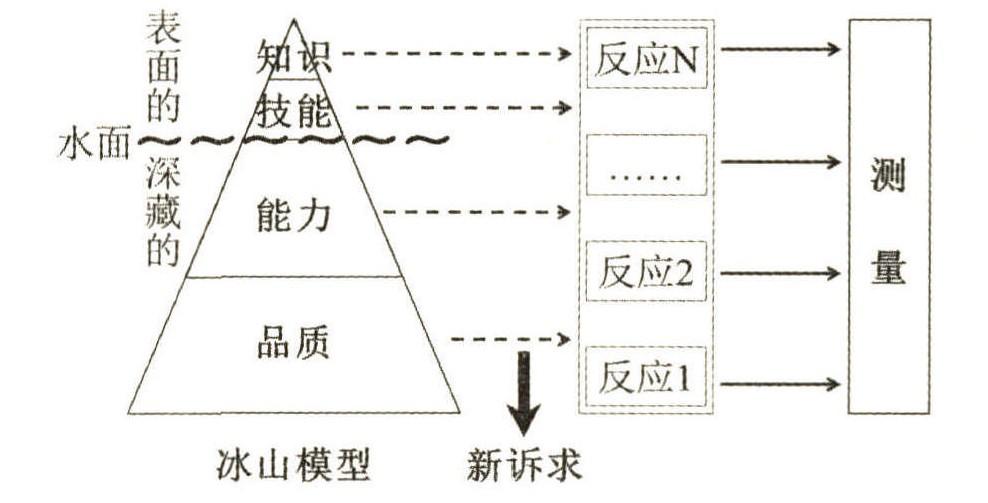
图 2 智慧教育对精准教学核心机制的新诉求
智慧教育不仅注重知识技能的传授,而且更加注 重能力品质的培育。 根据冰山模型可知 [9-10](图 2 左 侧),知识技能在水面以上,是表面的,容易被观察与 测量;能力品质在水面以下,是深藏的,不易被观察与 测量。 对知识技能和能力品质的测量,主流的理念为: 制定表征学习行为或结果水平状态的量规或指标体 系等标准,然后依据量规或指标体系设计问卷或试题 等工具以收集学生的反应数据,最后用统计学方法将 收集的数据进行分析, 并与量规或指标体系比对,从 而完成评估(图 2 右侧)。 目前,精准教学的以测辅学 机制也是采用这种理念。 然而,智慧教育不仅关注知 识技能,而且更加注重能力品质。 由知识技能跃升至 能力品质是质变的过程。 这一质变背后蕴含的内部心 理构念是统计学无法回答的难题。 此外,学生在问卷 或试题等测量工具中的反应数据所表征的实质意义, 也是统计学无法回答的难题。 例如,测量空间能力的
试卷所表征的空间能力具体指什么,它具有哪些属性 或变量,每道试题是对空间能力的哪个或哪些属性或变量的表征,试题特征(难度、区分度等)与这些属性 和变量是如何匹配的? 这些实质意义的缺失,致使收 集到的数据无法精准反映学生的空间能力是显然的。 这类本质上的问题是数理统计无法解决的。 而这类问 题的解决是实现精准决策、精准辅助进而实现智慧型 人才培育的基础和前提。 因此,这是智慧教育必须解 决的关键问题,也是智慧教育对精准教学以测辅学的 核心机制提出的新诉求(如图 2 所示)。
二、精准教学的测量理念:以测识学
(一)测量属性的构念理论
针对智慧教育对以测辅学核心机制的新诉求,精 准教学的测量理念必须做到“以测识学”。 以测识学是 指测量工具所测的维度能真实表征知识技能或能力 品质属性的实质,以此达到真正认识学生的学习表现 及相应的心理构念。 构念理论驱动的心理与教育测量 学认为,构念(Construct)是所要测量的心理属性的实 质,因此,构念理论也称为心理属性的实质理论。 本质 上,构念与自然科学领域中的长度、质量等物理属性 一样,是对所研究对象的某种特征或特征间关系的概 念化的表征。 [11]而从数理统计的角度讲,构念可以看 作是刻画或描述心理现象或活动的理论变量[12]。 心理 构念是导致学生种种外在行为的特征,但心理构念是 潜变量,无法直接观测,所以学生的心理构念特征是 通过他们在各种观测变量上表现推测的。 [13]即构念理 论驱动的心理与教育测量学认为,心理构念是导致观 测变量上的表现的原因(由因及果),而观测变量上的 表现可反过来推断心理构念(由果溯因)[14]。 因此,构 念理论驱动的心理与教育测量学认为,心理构念和观 测变量是因果关系机制。 心理构念以及这种因果关系 机制,从行为主义角度看,即是刺激(测验项目)与反 应(学习表现)间的联结机制,由此联结也从“黑盒”转变为“白盒”。
心理构念以及这种因果关系是智慧教育对精准 教学的核心机制新诉求得以实现的根基与支柱。 由此 也可以看出,构念理论理应是测量理论的前提,且能 弥补数理统计无法解决的所测属性的实质问题。 对 于构念理论,需要解决以下四个问题[11]:①构念的内 涵和外延;②构念的构成 、 维度或结构 ;③不同构念 水平的表现特征; ④不同构念水平的发展机制。 例 如,在设计测量学生的空间能力的工具前,首先要明 确一般情况下 , 空间能力 ( 所测构念 ) 指个体理解或 记忆各种对象间空间关系的能力 [15](对应问题①)。 当采用心理旋转任务测量空间能力时, 根据心理旋 转任务的信息加工模型可知(图 3 左侧)[16],空间能力 包含“编码、心理旋转、比较”三个认知成分(对应问题②)。 其中编码指识别图形的构成成分,以及它们的空 间关系;心理旋转指选定某一参照点,将其中一个图 形心理旋转至另一图形的相同方位上; 比较指依次 比较两图形间的构成成分。 每个认知成分均有与之对 应的表现特征(对应问题③),与编码对应的表现特征 是“图形复杂度”;与心理旋转对应的表现特征是“角 度分离程度 ”; 与比较对应的表现特征是 “ 图形复杂 度”和“图形相同或不同”。 且这三个认知成分是按照 顺序发展的(对应问题④)。 顺序发展的认知成分表征 构念的不同水平。 通过对空间能力的构念理论分析, 可以明确所测构念和任务反应间的关系(图 3 中侧所 示)[11], 即可以清楚地认识学生不同的任务反应背后 的实质意义。 接下来,测量工具的设计就变为依据所 测构念的不同水平和与之对应的表现特征(从任务角 度看,即为任务特征)进行的不同测量任务的设计。 图 3 右侧为依据上述的空间能力构念理论设计的一个 任务, 该任务是新课标人教版六年级数学下册 93 页 的第 4 题[17]。
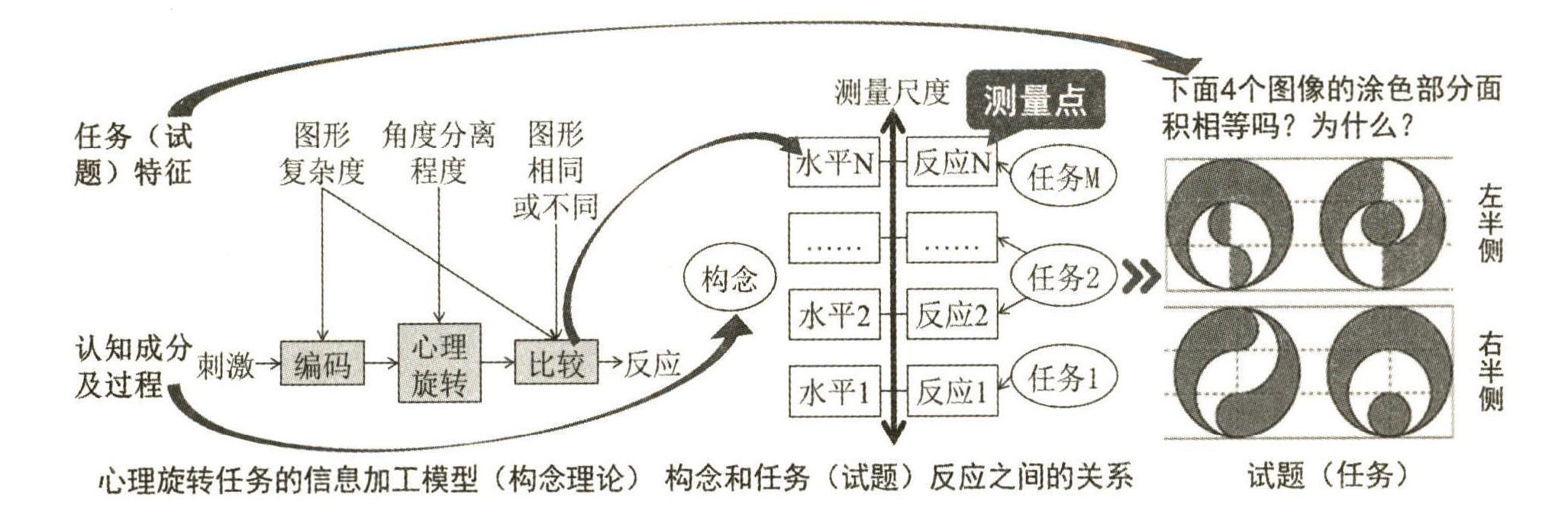
图 3 构念理论驱动的测量
(二)精准教学的计量指标:流畅度
在构念理论驱动下,精准教学的观测指标(即观测 变量,构念理论层面)是由所测构念决定的。 而对于每 个观测指标的计量, 精准教学采用流畅度作为表征学 生学习发展的计量指标(测量理论层面)。 流畅度是指 学习表现的“准确度”和“速度”[5]。 由此可以看出,精准 教学所信奉的知识技能或能力品质的真正掌握不仅体 现在学习表现的质量和准确度上,也体现在速度上[18]。 其中,准确度有两个子指标:正确反应和错误反应。 这 比目前教育测量与评估中主流的以测验得分或正确 率作为计量指标,更能全面地衡量学生的表现。 此外 速度指标可衡量学习表现 (包括正确反应和错误反 应)的敏捷性和流利度,因此,速度指标的引入使得测 量所得的数据更接近学生的实际水平。 另外,流畅度 的“正确反应”、“错误反应”和“速度”等三个子指标的 配合使用,可较为精确地检测出学生在测试中是否存 在蒙猜现象(比如学生反应速度异常快,但错误反应 很高、正确反应很低,这种情况蒙猜的可能性极大), 甚至能检测出是否存在抄袭现象(比如,学生反应速 度异常快,且基本保持匀速,正确反应和错误反应与 其他学生极其相似,这种情况抄袭的可能性很大)。
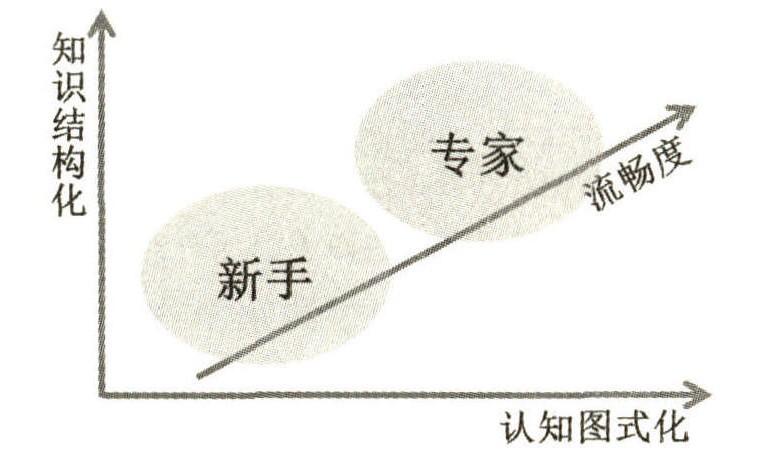
图 4 专家—新手流畅度不同的归因
认知心理学家和神经科学家有证据表明,大脑不 同的“行为”产生了流畅度的系列特点[19]。 因此,学习 表现的不同流畅度是学生内部认知与构念的反映。 专 家—新手的相关研究表明,二者在知识的结构化程度
(可表征知识技能)和认知的图式化程度(可表征能力 品质)方面是不同的(如图 4 所示)。 在知识的结构化 程度方面, 新手在某个领域的知识技能偏于零散孤 立,对核心的概念、原理的理解一般处在表层,专家在 某个领域的知识技能偏于高度结构化、组织化,对核 心的概念、原理的理解一般处在较深层面。 [20]而知识 技能按照某种意义的结构化、组织化,使得大量的领 域问题对专家来说变得熟知,专家可迅速再认和理解
问题背后蕴含的规则,抓住问题的本质和结构,第一 时间作出更为正确的反应。 因此,知识的结构化程度与流畅度是正相关的。 在认知的图式化程度方面,新 手没有形成或拥有较少的认知图式(即认知图式化程 度低),在解决问题过程中,新手需要将领域问题逐步 转译成内部表征,并按照相应的心理构念一步一步地(即解题步骤)作出外在反应,从而解决问题。 这样的 问题解决过程需要高强度地使用短时记忆,因此伴有 较高的认知负荷[21]。 而专家拥有大量的认知图式(即 认知图式化程度高), 领域问题的表征和解决过程变 为模式识别的过程。 认知图式提供了整合问题模型的 模板,有利于激活长时记忆中与领域问题相匹配的解 决策略,从而大大降低了认知负荷。 [22]因此,在解决领 域问题时,专家基于认知图式可快速、精准地提取相 关信息, 筛选对应的解决策略。 由此可知,认知的图式 化程度与流畅度也是正相关的。
由于知识的结构化程度在某种程度上可表征知 识技能的水平, 认知的图式化程度在某种程度上可 表征能力品质的水平, 所以流畅度可以表征知识技 能和能力品质的水平, 所以流畅度可以表征知识技 能和能力品质的水平。 如果智慧教育,从布鲁姆认知 领域目标分类理论 ( 修 订 版 )[23] 的三角模型来解读 , 则其目的是以底三层目标为基底, 重点发展顶三层 的目标。 [24]而流畅度则为智慧教育的这个目的提供 了可能的思路。
三、精准教学的记录技术:以绘视学
由上述分析可知,构念理论和流畅度的融合使得 精准教学能够以测识学。 接下来的问题是:测量后,所 得的学生表现数据如何记录? 为了解决这个问题,需 要解决以下两个子问题:①流畅度的三个指标如何组 合生成记录指标;②记录指标确定后,数据应该记录 在哪里,以什么方式记录? 对此,精准教学采用自有 的一套记录技术,以实现“以绘视学”的理念。
(一)精准教学的记录指标:频率
图 5 从流畅度到频率
如图 5 所示, 流畅度具有 “正确反应”、“错误反 应”和“速度”等三个指标,那么这三个指标如何配合使 用呢? 众所周知,“速度”在数学和物理学中常使用“单 位时间”表征,因此可以尝试使用“正确反应频率=正确 反应/测量时间” 和 “错误反应频率=错误反应/测量时间”来代替流畅度原有的三个指标。 频率指单位时间内某事件重复发生的次数。 这里的“事件”在精准教学 中指学习表现,即精准教学中的频率指单位时间内正 确反应和错误反应发生的次数。 因此,频率可以同时 体现流畅度所要求的“准确度”和“速度”,可以作为精 准教学的记录指标。 也就是说,正确反应频率和错误 反应频率替代流畅度原有的三个指标具有一定的合 理性。 需要说明的是,精准教学中的学习反应频率具 有两层含义:①行为的频次,如 1 分钟内正确阅读英 语单词的数量;②单位时间的行为贡献(或称行为价 值),如 1 小时内学生获得的测试分数。 在实际的教学 过程中,可以根据需要自由选择。 在其他条件相同的 情况下,精准教学认为,流畅的学习表现比不流畅的 表现更有可能在未来发生。 而频率作为流畅度的主要 记录指标,相比测验得分或正确率,更能精准地预测 所测学习表现未来发生的概率。 因为正确率相同而频 率不 同[25] 是 很 常 见 的 , 而这种情形反映出的学生 水 平显然是不同的,未来发生的概率自然也不会相同。
(二)精准教学的记录图表:课时标准变速图表
记录指标确定后,那么测量所得的数据该记录在 哪里,以什么方式记录呢? 对此,精准教学使用标准变 速图表作为记录工具。 标准变速图表是一种半对数图 表,可实现学生实时表现数据的可视化。 在精准教学 中,主要使用课时标准变速图表(以下简称课时变速 图) 和日常标准变速图表 (以下简称日常变速图)两 种。 其中,课时变速图用于某一节课或者某一教学片 断中。 图 6 为课时标准变速图表的模板和相应的绘制 规范。 横轴是课时轴,相邻两条粗垂线间表示一节课 或一个教学片断。 每条垂线代表一次测量,是测量标 记线。 横轴使用分度均匀的等距坐标轴。 相邻两条粗 垂线间被九条细垂线分成 10 个间隙,如果需要,每个 间隙内可进行一次辅助,每次辅助需用垂直的变相线 标注,并说明辅助的详细信息。 因此,每节课或教学片 断内最多进行十次辅助。 纵轴是频率轴,用于表征学 生每分钟的学习反应的数量(当测量时间不是 1 分钟 时, 需要进行转换)。 精准教学认为学习表现频率从 50 增至 100 和从 100 增至 200,学生的学习进步程度 是一样的,都是 2 倍。 [26]即精准教学是按照比例尺度 来衡量学习发展的。 然而,图表的两刻度间的差量均 遵循“相减”规则,因此,课时变速图的纵轴改等距坐 标为对数坐标。 这样测量所得的频率数据实际是以频 率的对数的形式记录在课时变速图上的。 例如,当频 率 50 标记在表示 50 的频率刻度(频率刻度在图表左 侧的纵轴上)上时,实际是 lg50。 因此,图表中 100 与50 间 的 差 量 实 际 是 lg100 与 lg50 的 差 量 (lg100 -lg50 = lg(100/50) ),这样在不违背 “ 相减” 规则的前 提下,巧妙地完成了等距尺度向比例尺度的转变。 另 外,为了能够在图表中表示更为宽泛的频率范围,纵 轴 分 为 三 个 半 周 期 , 周 期 间 采 用 比 例 刻 度 (0.1,1,10,100)、等距坐标,周期内采用前述的对数 坐标、等距刻度(10,20,…,100)。 当然这牺牲了一定 的记录精度(每个顶层的周期内的精度都是其相邻底 层周期内精度的 1/10),然而这是值得的。 因为频率越 大,相邻的两频数(如 100 和 101)所表征的学习进步 量越小,并且如果不降低精度,水平刻度线将会越来 越密集,由此也使得图表越来越难以绘制。 从这个角 度讲,纵轴采用此方式是一个明智之举,它用极低的 成本获得了巨大收益!
图 6 课时标准变速图表模板与绘制规范
需要注意的是, 图表中的水平线有两种含义:① 按照图表左侧纵轴的刻度,水平线表征学习反应的频 率;②按照图表右下侧测量时间的刻度,水平线表征 测量持续的时间。 测量时间的刻度用于绘制每次测量 的“记录地板”,使用短线“-”符号绘制。 记录地板也有 两层含义:①表征测量持续时间;②更为重要的是,表 征测量的精度。 例如图 6 中每次测量的记录地板均在 15 秒的刻度线上, 这意味着每次的测量的时间均持 续 15 秒, 如果相邻两次的学习反应间隔在 15 秒内, 则可以准确测量,如果间隔超过 15 秒,则无法准确测 量。 也就是说,图 6 中每次的测量精度均为每 1/15 次/ 秒,转换成分钟单位后,该精度变为 4 次/分,正好对 应左侧的频率刻度,这就是同一水平线能够表征两种 含义的原因。
在绘制时,首先在“课时信息”区域对课程或教学 片断的日期、名称、开始和结束时间作个说明,之后在 “基本信息”区域注明管理者 、 监督者、 技术者、 计数
者、绘制者、执行者(即被测者)等信息,然后使用目标框符号“□”在对应的垂线和水平线的交汇处绘制本 节课或教学片断的目标。 对于每次测量均需要做三件 事:用符号 “·”绘制正确反应频数 ;用符号“×”绘制错 误反应频数;用短线“-”绘制记录地板。 此处需要注意 的是,当频率值低于记录地板时,需采用符号“? ”表 示,这是因为受测量精度限制,而无法精确测量的缘 故,此种情况多出现在错误频率为 0 时(另一个原因 是标准变速图表没有频率为 0 的刻度线,因为对数的 定义决定了不存在 lg0)。 第一次测量结束后,需要在 正确频率圆点和目标框间绘制一条直线,这是一条最 小变速线,表示学生最小的进步速度。 当正确频率点 连续两次处于最小变速线下方时,需要立即启动决策 机制,制定相应的辅助策略,每次辅助需用变相线标 注,并对辅助策略进行说明。
(三)精准教学的记录图表:日常标准变速图表
图 7 日常标准变速图表模板与绘制规范
在课堂或教学片断结束时,需立即将课时变速图 显示的该堂课或教学片断最好的那次测量转绘至日 常变速图中。 图 7 为日常标准变速图表的模板和相应 的绘制规范。 横轴是时间轴,共 140 天,约 1 学期的时 间跨度,相邻两粗垂线间表示 1 周的时间。 纵轴基本 和课时变速图一致,不同之处是日常变速图为了增大 可表示的频率范围,周期扩至六个,这样最低可记录 24 小时发生 1 次的反应, 最高可记录每分钟 1000 次 的反应,基本上能够满足大多数学习情况。 其他诸如日 期信息、测量时间等信息和课时变速图基本一致。 学习 反应频率的绘制也基本和课时变速图一致, 不同之处 是发展变速线的绘制方法。 在学习之初, 绘制者需用 “A”配以目标框“□”在对应的垂线和水平线的交汇处 绘制教学目标, 一般学习一周后开始绘制发展变速 线(课时变速图中是第一次测量后绘制 ), 发展变速线的绘制主要有两种方法:①目测法,即通过观察粗略绘制;②精准法,如统计学使用的绘制线性回归的 方法。 有数据显示,目测法可以近似产生同样有效的数 据分析和辅助[27]。 之后每一次测量后,均需要修正发展 变速线。 当连续两次测量均使得目标框在发展变速线 左上方时,需要立即启动决策机制,制定相应的辅助 策略,并用变相线标注与说明。 辅助之后,需要按照前 述的规则重新绘制一条新的发展变速线,并且绘制新 的发展变速线时一般不会考虑辅助前学生的反应频 率。 在判定学生学习的发展情况或判定目标框在发展 变速线的哪一侧时,日常变速图提供了变速线基板作 为辅助工具,从而提高速度和精准度。
四、精准教学的决策机制
智慧教育境域中精准教学的主要任务是:①判定学习是否发生;②预判学习能否按期完成;③如果不能完成,决策如何辅助。 而这将涉及前述的变速线的内涵和作用。
(一)精准教学的决策依据:变速线
标准变速图不仅仅用于呈现学生的学习表现,它 的另一个更为重要的使命是标定或表征学生的发展情 况,并以此作为后续决策的依据。 而这个使命是通过变 速线(包括最小变速线和发展变速线)实现的。 精准教 学认为学习是学生表现随时间的发展变化, 在标准变 速图中即为学习反应频率随时间的发展变化。 这个变 化通过两种方式表示: ①第一次测量的正确反应频率 圆点与目标框间的连线,即最小变速线,用于课时变速 图中; ②用一条贯穿于所绘制的反应频率的数据的直 线表示的,这条直线就是发展变速线,用于日常变速图 中。 一般发展变速线成对出现,一条表示正确反应频率 随时间的发展变化, 另一条表示错误反应频率随时间 的发展变化。发展变速线的斜率表征学生的学习速度, 以正确反应频率的发展变速线为例,斜率较大表明学 习速度较快; 斜率较为平坦表明学习几乎没有发生; 斜率为负值表明学生在退步[28]。
其实,变速线本质上是对所测构念的发展变化趋 势的可视化标定或表征,它将智慧学习所要培育的构 念转换成易于理解、易于操作的形式,传达给决策模 型,以此指导精准教学进行决策。 如图 8 所示,由所测 构念到变速线再到决策模型,其实是智慧教育诉求由 内隐逐层外显的过程,也是以测辅学机制的“神经系 统”,以测辅学机制的三要素就是在这个“神经系统” 的作用下得以 “运转”。 而无论是智慧教育诉求的外 显,还是以测辅学机制的运转,关键一环即为变速线。
众所周知,心理学和教育学领域中的个体属性(无论是知识技能还是能力品质)通常都是潜在的、内隐的, 无法直接观察与测量,而变速线提供了将个体的内隐 属性进行外显的技术,并将所测构念与决策模型连通 起来。 从这个角度讲,变速线可以作为精准教学可行、 合理的决策依据。

图 8 变速线作为决策依据的原理
(二)精准教学的决策模型
前面定性地表述了发展变速线斜率与学习速度 的关系,而要完成智慧教育境域中精准教学的三个主 要任务,需要有明确的判定依据。 为此,笔者设计了图 9 所示的精准教学的决策模型,该模型主要有三个维 度:决策时机、辅助策略和以测辅学三要素。 决策时机 有三个,分别是事前、事中和事后。 辅助策略遵循干 预—反应模型,随着决策轨迹循环次数的增加,循证 干预的强度将逐步增加, 并且辅助也越发专业化、智 能化(如从微课助学到精准帮学)。 而以测辅学三要素 维度规定了决策轨迹的每次循环需经历的 “测量”、 “记录”、“决策”三阶段和路径。
 图 9 精准教学的决策模型
图 9 精准教学的决策模型
事前决策一般是指学前对学生的预备知识的诊 断,选用课时变速图作为记录工具并遵循它的绘制规 范。 事前决策一般作三次测量,如果三次测量的均值 大于目标框的值, 说明学生具有新课需要的知识储 备,相应的辅助策略则为新课程的学习,否则说明学 生不满足学习新课的先决条件,相应的辅助策略为重新学习未掌握的知识。 事中决策一般是指学习时对学 生进行实时的测量监控,依然选用课时变速图。 学习时,学生的学习表现一般有以下四种(如图 10 所示)。 第四种情况说明学生已达到目标,相应的辅助策略是 新课程的学习。 第二种情况说明学生可按期完成目 标,继续按此教学策略学习即可。 第一种情况显示学 生最后两次测量的正确反应频率均在最小变速线右 下方,可以先给予简单的辅助,如重新讲解、微课辅助 等。 如果随后学生的反应频率在最小变速线的左上 方,说明辅助策略有效,后续沿着当前的教学策略继 续学习。 如果随后学生的反应频率依然在最小变速线 的右下方,就会出现第三种情况,此时已是第二次辅 助,根据干预—反应模型,需要给予更为专业化、智能 化的辅助(如精准推送学习资源)。 如果这节课或教学 片断已结束,学生的学习依然没有达到目标,则需要 将学生表现最好的那次测量转绘至日常变速图中以 便进行事后决策。 事后决策一般是指某节课或教学片 断结束后对学生学习表现的判定或预判。 事后决策选 用日常变速图作为记录工具并遵循它的绘制规范。 判 定学习是否发生和预判学习能否按期完成,主要依据 目标框“□”在发展变速线的哪一侧。 如果学生反应频 率值高于目标框的值,说明学生已完成目标,可以进 入新课程的学习;如果目标框在发展变速线上或在发 展变速线下侧, 说明学生可按期或提前完成目标,此 时按照当前教学策略继续学习即可;其他目标框的位 置情况均说明学生无法按期达成目标,因此,需要依 据干预—反应模型制定对应的辅助策略进行辅助,有 时甚至需要借助外部力量和技术的帮助,如向外部系 统定制专属的教学策略。 需要特别说明的是,辅助的 强度、 专业化是依据辅助策略的循环次数而定的,而 不是依据决策时机而定的。 另外,每次辅助均需要新 一轮的测量、记录和决策循环,因此,决策的轨迹总体 上是由内而外、呈螺旋线发展的。
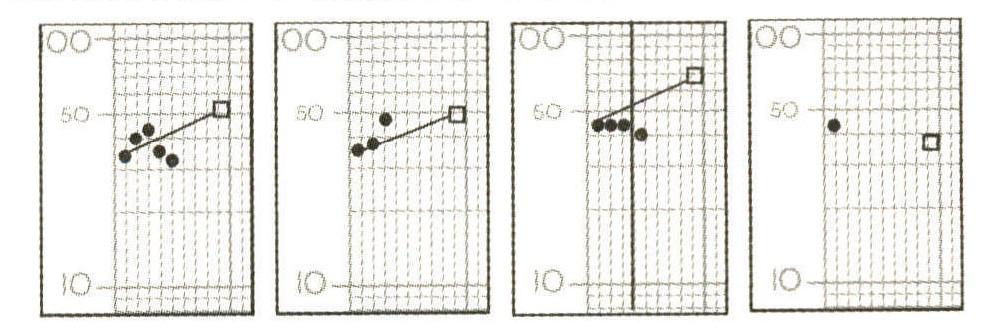
图 10 学习过程中学生的四种学习表现
(三)精准教学的辅助案例:习题的精准推送
信息技术支持的智慧教育的其中一个目标是实 现“高效减负”。 而高效减负必须要抛弃现有的“题海 战术”策略,让学生只做该做的习题。 对此,接下来将 以空间能力的练习为例,论述精准教学中关于“习题
的精准推送”辅助策略。 通过对图 3 的解析,可以确定 旋转任务中的空间能力主要有三个认知成分: 编码、心理旋转和比较。 编码对应的习题特征是图形复杂 度,心理旋转对应的习题特征是角度分离程度,比较 对应的习题特征主要是比较图形相同还是不同,当然 也和图形复杂度有关。 由此,习题的精准推送机制的 第一步是准备足量的习题,并作标注。 即事先准备足 量的、类似的旋转任务存于习题库中,并以这三个认 知成分为标签标注这些旋转任务的特征,如旋转任务 的角度分离程度的水平(它反映的是心理旋转认知成 分的水平)。 第二步是测量分析学生的反应。 即当学生 做这套旋转任务习题集时,精准教学会自动测量学生 在每道题中的反应,随着学生做题数量的增加,精准 教学可通过上述的决策机制,准确地判定学生在各个 认知成分中的水平以及学生最薄弱的认知成分。 第三 步是精准推送习题, 即针对学生最薄弱的认知成分, 精准推送习题。 推送原则为:以最薄弱的认知成分对 应的习题特征为变量(如角度分离程度),其他两个认 知成分对应的习题特征(如图形复杂度,比较图形相 同还是不同)为常量,推送在薄弱认知成分对应的习 题特征(如角度分离程度 ) 上的、 具有不同难度水平 (按照水平由低至高的顺序推送)的习题集,直到学生 的反应频率达到目标的要求。
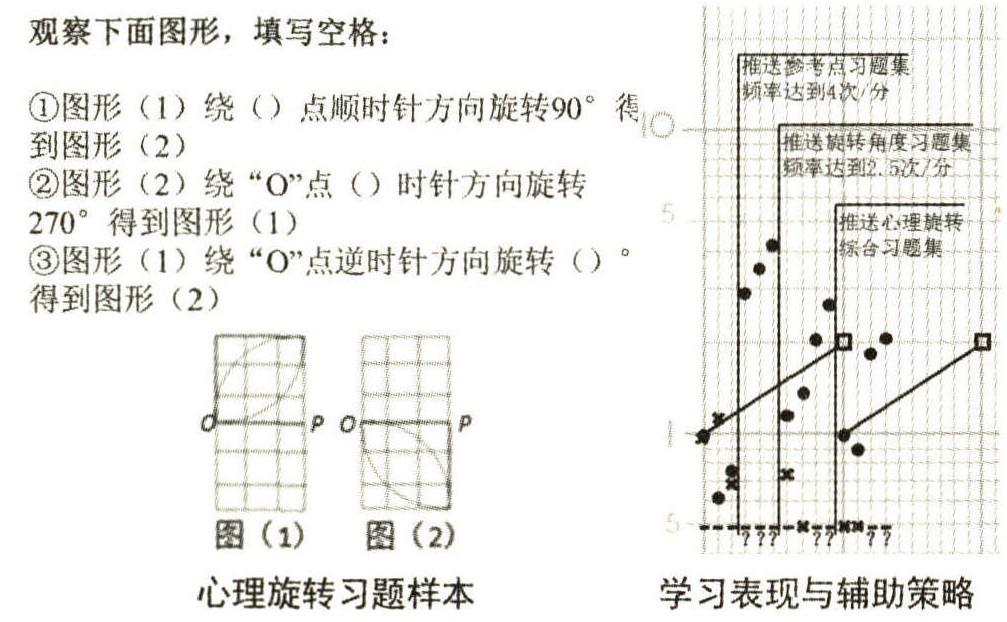
图 11 心理旋转习题和相应的学习表现与辅助策略
图 11 右侧图表是测量某五年级学生做心理旋转 习题集的反应记录,使用的是课时变速图,每次测量 时间均为 2 分钟,频率目标为 2 次/分。 最初学生练习 的心理旋转习题集样本如图 11 左侧所示, 编码方面 的习题特征水平是图形只有一个构成成分(花瓣状图 形),且处于同一平面;心理旋转方面的习题特征水平 是考察参照点的选定以及相应的旋转角度确定,其中 旋转角度范围是 0~360°;比较方面的习题特征水平是 比较两个图形旋转后是否重合(即比较相同)。 图 11 右侧图表中的前三次测量显示,后两次学生的反应均 低于最小变速线, 由上述精准教学的决策机制可知, 需要进行相应的辅助, 这里采用习题的精准推送策 略。 图 11 左侧的习题集样本在编码和比较两个认知 成分中的难度处于较低水平(编码方面只有一个构成 成分,且处于同一平面;比较方面直接比较相同),并 且学生已掌握了这两方面的技能。 因此,推送的习题 在编码和比较两方面的习题特征与图 11 左侧的习题 集样本相同且保持不变,在心理旋转认知成分方面分 三个难度水平:①旋转参照点的练习;②旋转角度的 练习; ③心理旋转综合练习。 习题集样本如图 12 所 示。 学生在推送的习题集中的反应如图 11 右侧图表 所示。 第一次推送参考点习题集(图 12 左上侧所示), 第三次测量显示学生达到要求的 4 次/分的频率。 第 二次推送角度旋转习题集(图 12 左下侧所示),第四 次测量显示学生达到要求的 2.5 次/分的频率。 第三次 推送心理旋转综合习题集(图 12 右侧所示),并按课 时变速图绘制规范重新绘制最小变速线, 测量显示, 该学生在第二次的测量低于最小变速线(不需辅助), 后两次的测量高于最小变速线,且最后一次测量达到 预设的目标:2 次/分。 通过在心理旋转认知成分方面 的习题精准推送,该五年级学生达到了所要求的流畅 度目标,接下来便可进入下一知识的学习。
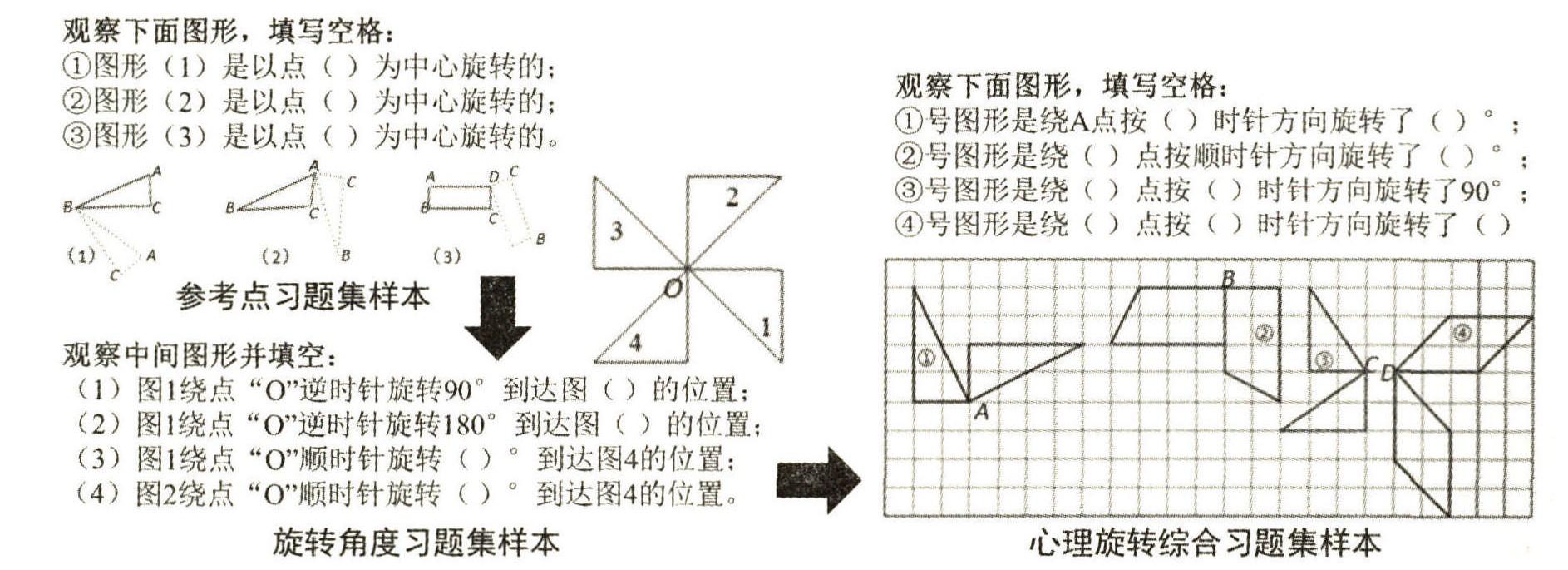
图 12 心理旋转习题的精准推送
五、结 语
从早期的精准教学到信息技术支持的精准教学, 以测辅学一直是精准教学的核心机制。 不过在智慧教 育境域中,精准教学需要满足智慧教育提出的新诉求, 因此,精准教学需要做到“守正出新”。 对此,本研究以 智慧教育新诉求为导向, 结合心理与教育测量学中的 构念理论,较为深入、全面地透析了精准教学“以测辅 学”的机制与原理,包括测量时的“以测识学”的原理, 记录时的“以绘视学”的原理和决策时的“以评辅学”的 原理。 这些原理从某种程度上也解释了任务刺激与学 习反应之间的关联机制, 使得精准教学可以对所测构念、任务特征、学生反应及三者间的关系给予合理的解 释。 另外,通过上述对精准教学的核心机制的解读,可 以总结出以测辅学的具体操作步骤如下: ①明确所测 构念的实质含义及认知模型或过程; ②解析认知模型 或过程中蕴含的认知成分所对应的任务特征; ③依据 任务特征设计和标注测试任务; ④用课时变速图记录 课堂或教学片断中学生的表现; ⑤每节课或教学片断 后, 用日常变速图记录学生在该节课或教学片断中最 好的学习表现; ⑥实时对④和⑤中绘制的表现进行决 策,必要时给予相应的辅助。 在此研究的基础上,我们 后期将进一步开展在智慧教育理念下精准教学的辅助 架构的研究,以期更好地为智慧教育和智慧学习服务。
[参考文献]
[1] 彭红超, 祝智庭. 面向智慧学习的精准教学活动生成性设计[J]. 电化教育研究,2016(8):53-62.
[2] 祝智庭, 彭红超. 信息技术支持的高效知识教学:激发精准教学的活力[J]. 中国电化教育,2016(1):17-25.
[3] LAMBE D, MURPHY C, KELLY M E. The Impact of a precision teaching intervention on the reading fluency of typically developing children[J].Behavioral interventions,2015,30(4):364-377.
[4] BINDER C, WATKINS C L. Precision teaching and direct instruction: measurably superior instructional technology in schools [J].
Performance improvement quarterly,2013,26(2):73-115.
[5] BINDER C. Precision teaching: measuring and attaining exemplary academic achievement[J].Youth Policy,1988,10(7):12-15. [6] 祝智庭, 贺斌. 智慧教育:教育信息化的新境界[J]. 电化教育研究, 2012(12):7-15.
[7] BINDER C, WATKINS C L. Precision teaching and direct instruction: measurably superior instructional technology in schools [J].
Performance improvement quarterly,1990,3(4):74-96.
[8] JOHNSON K, STREET E M. From the laboratory to the field and back again: morningside academy's 32 years of improving students' academic performance[J].The behavior analyst today,2012,13(1):20.
[9] MCCLELLAND D C. Testing for competence rather than for “intelligence”[J].American psychologist,1973,28(1):1.
[10] SPENCER L M, SPENCER S M. Competence at work: models for superior performance[M]. Manhattan:John Wiley & Sons,1993. [11] 杨向东.理论驱动的心理与教育测量学[M].上海:华东师范大学出版社,2014.
[12] WHITELY S E. Construct validity:construct representation versus nomothetic span[J].Psychological bulletin,1982,93(1):179-197. [13] 杨向东.教育测量在教育评价中的角色[J].全球教育展望,2007,36(11):15-25.
[14] KOZAK M J, MILLER G A. Hypothetical constructs versus intervening variables: a re-appraisal of the three -systems model of anxiety assessment[J].Behavioral assessment,1982,4(3):347-358.
[15] LOHMAN D F, PELLEGRINO J W, ALDERTON D L, et al. Dimensions and components of individual differences in spatial abilities[M]. Intelligence and cognition: contemporary frames of reference. Springer Netherlands, 1987:253-312.
[16] LOHMAN D F, IPPEL M J. Cognitive diagnosis: from statistically based assessment toward theory-based assessment [J].Test theory for a new generation of tests,1993:41-71.
[17] 电子课本网. 2. 图形与几何 (第 93 页)—人教版六年级下册数学电子课本.[EB/OL].(2016-09-25)[ 2016-09-25]. http://www. dzkbw.com/books/rjb/shuxue/xs6x_new/098.htm.
[18] HAUGHTON E. Great gains from small starts[J].Teaching exceptional children,1971,3(3):141.
[19] POLDRACK R A, SABB F W, FOERDE K. The neural correlates of motor skill automaticity [J].The Journal of Neuroscience, 2005,25(22):5356-5364.
[20] PELLEGRINO J W E, CHUDOWSKY N E, GLASER R E. Knowing What students know: the science and design of educational assessment[M].Washington, D.C.: National Academies Press,2001.
[21] SWELLER J. Cognitive technology: Some procedures for facilitating learning and problem solving in mathematics and science[J].
Journal of educational psychology,1989,81(4):457.
[22] 杨向东. 代数应用题项目生成中的认知过程与任务特征分析[J]. 心理科学进展, 2013, 21(1):175-189.
[23] ANDERSON L W, KRATHWOHL D R, BLOOM B S. A taxonomy for learning, teaching, and assessing: a revision of Bloom's taxonomy of educational objectives[M]. Boston:Allyn & Bacon,2001.
[24] 祝智庭. 智慧教育新发展:从翻转课堂到智慧课堂及智慧学习空间[J]. 开放教育研究, 2016(1):18-26.
[25] BARRETT B H. Communitization and the measured message of normal behavior [J].Teaching the severely handicapped,1979 (4): 301-318.
[26] WHITE O R. Precision teaching—Precision learning[J].Exceptional children,1986,52(6):522-534.
[27] HARING N G, LIBERTY K A, WHITE O R. Rules for data-based strategy decisions in instructional programs: current research and instructional implications [M]//SAILOR W, WILCOX B, BROWN L. Methods of instruction for severely handicapped students. Baltimore:Paul H. Brookes,1980:159-192.
[28] CALKIN A B. Standard Celeration Charting[M]. Encyclopedia of Child Behavior and Development. Springer US, 2011:1432-1435.
Measurement-assisted Learning:A Core Mechanism of Precision Instruction in Smart Education
PENG Hongchao1, ZHU Zhiting2
(1.Department of Education Information Technology, Faculty of Education, East China Normal University, Shanghai 200062; 2.School of Open Learning and Education, East China Normal University, Shanghai 200062)
[Abstract] The mechanism of measurement-assisted learning of precision instruction just focuses on learners' behaviors. But smart education has new demands for teaching and learning evaluation: to understand the essence of the measured construct. Therefore, this study, guided by the demands of smart education, combined with construct theory in psychological and educational measurement, analyzes the mechanism and principle of measurement -assisted learning of precision instruction in smart education
deeply and comprehensively from three elements (i.e., measurement, recording, decision -making). The principles are as follows: the principle of "understanding learning via measuring" during measurement ( the essence of measured construct and fluency as indicators), the principle of " visualizing learning via drawing" during recording ( frequency as recording indicator and standard celeration chart as recording chart), and the principle of " assisting learning via evaluating" during decision-making ( celeration line as decision-making basis, decision-making model and assisting mechanism ). Finally, specific operation steps are summarized for the purpose of providing guidance and reference for future precision instruction.
[Keywords] Smart Education; Precision Instruction; Construct Theory; Fluency; Standard Celeration Chart
